[백준]BOJ 11053 - 가장 긴 증가하는 부분 수열 5 - C++/DP

https://www.acmicpc.net/problem/14003

14003번: 가장 긴 증가하는 부분 수열 5

 
<문제>

 
<풀이>
LIS(Longest Increasing Subsequence)라고 하는 유명한 DP 문제이다. 이 문제 외에도 연계된 문제들이 많으니 1번(BOJ 11722)부터 차례대로 풀면 어느새 여기까지 풀게 된다.

이 문제들은 총 2가지 기준으로 분류된다. 첫 번째 기준은 O(n²), O(nlogn) 두 번째는 LIS 출력 여부이다. 이 중에 O(nlogn) 알고리즘을 사용하고 LIS를 직접 출력해야 하는 문제가 이 문제이다. 원래는 Swift로 작성하려 했지만, 백준의 입력시간 문제 때문에 Swift론 입력 횟수가 적은 O(n²)문제를 풀고 O(nlogn) 문제는 C++로 작성하였다.
 
기본적인 알고리즘 콘셉트는 다음과 같다.

1. 수열 a, 순서를 저장할 order, 그리고 dpTable까지 세개의 배열(리스트, 벡터...)이 필요하다. 

2. dpTable에는 각 인덱스에 대응하는 숫자 크기의 LIS를 형성 할 수 있는 원소의 최소값이 저장된다
- 글로 쓰면 설명하기 어려우니 아래에 표로 그리겠다.

3. 수열 a를 전체 순회하면서 원소 a[i]가 마지막 값인 최장 부분 수열의 길이 order[i]를 채운다.

4. order[i]를 만들기 위해선 dpTable에서 본인보다 크거나 같은 원소를 가진 인덱스의 최소값을 찾아야 한다. 이 때 이진 탐색을 이용하면 O(logn)시간 내에 최소값을 찾을 수 있다.

5. 순회가 끝났다면 order[i]에 저장된 값중 최대값이 수열 a의 LIS의 길이이다.

6. 이 때 LIS를 직접 출력 하고 싶으면, order를 거꾸로 탐색하여 찾는다 (앞부터 탐색하면 LIS를 출력 할 수 없으니까)

글로 설명하려니 복잡한데 그냥 표로 표시하면 다음과 같다.

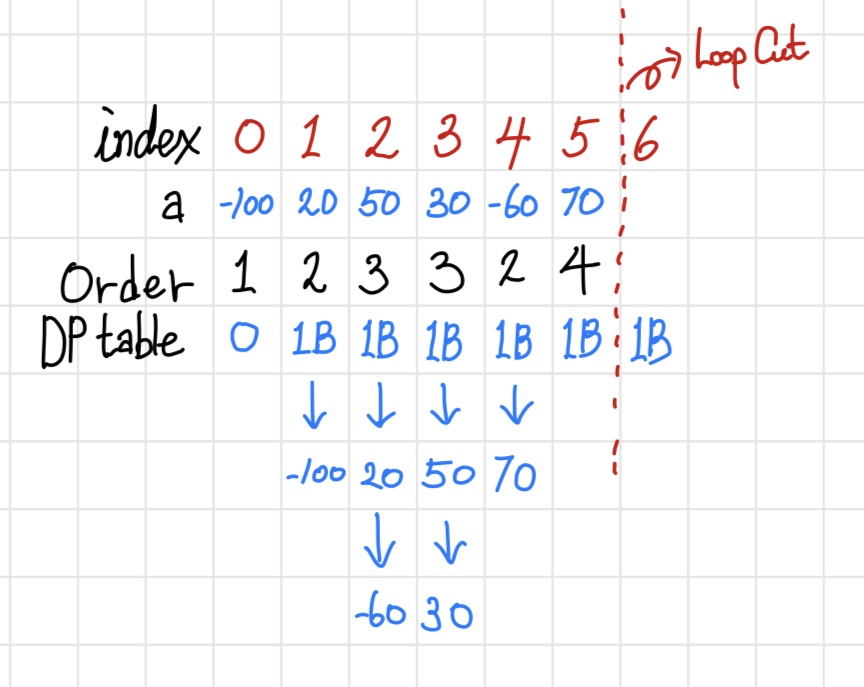
1. 처음에 dpTable은 max보다 큰 수로 초기화 한다. 표에선 1B라고 적어놨는데 1B + 1이 맞다.
2. dpTable에서 a[i] 보다 크거나 같은 수가 저장된 인덱스 중 가장 작은 인덱스를 이진 탐색으로 찾는다.
3. 찾은 인덱스를 bsidx라고 했을 때, dpTable[bsidx]를 a[i]로 갱신하고, order[i]에 bsidx를 저장한다.
- 코드에선 크기 비교를 하는데 차이는 없다. 코드를 작성 할 때 필요 없는 값 갱신을 줄이고 싶었는데 지금보니 갱신 몇 번을 줄이는 대신에 쓸모 없는 연산이 생겼다.
 
2~3을 반복하며 전체 순회를 하고 나면 max(order)가 LIS 길이의 최대값이 된다.
LIS를 직접 출력하려면 max(order)의 수를 줄여나가면서 역으로 순회하면 된다.
 
이 문제는 O(n²)의 풀이를 먼저 이해하고 와야 DP로 이해가 빠르다. 그것 때문에 문제를 5개로 쪼개서 낸 것이 아닐까.
 
<코드>
 
O(nlogn)

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int binarySearch(int n, int t, vector<int>* dpTable) {
    int low = 1, high = n, mid;
    while (low < high) {
        mid = (low + high) / 2;
        if ((*dpTable)[mid] < t) {
            low = mid + 1;
        }
        else {
            high = mid;
        }
    }
    return low;
}

int main(void) {
    int n, ai, bsidx;
    vector<int> a, order, dpTable;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> ai;
        a.push_back(ai);
    }
    dpTable = vector<int>(n + 1, 1000000001);
    dpTable[0] = 0;

    for (int i = 0; i < n; i++) {
        bsidx = binarySearch(n, a[i], &dpTable);
        if (dpTable[bsidx] > a[i]) {
            dpTable[bsidx] = a[i];
        }
        order.push_back(bsidx);
    }

    int max = *max_element(order.begin(), order.end());
    cout << max << endl;
    
    vector<int> lis;
    for (int i = n - 1; i >= 0; i--) {
        if (order[i] == max) {
            lis.push_back(a[i]);
            max--;
        }
    }
    
    for (int i = lis.size() - 1; i >= 0; i--) {
        cout << lis[i] << " ";
    }

    return 0;
}

 
O(n²) - 시간초과

#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;

int main(void) {
    int n, ai, max;
    vector<int> a, order, lis;
    cin >> n;
    for (int i = 0; i < n; i++) {
        cin >> ai;
        a.push_back(ai);
    }
    order = vector<int>(n, 1);

    for (int i = 0; i < n; i++) {
        for (int j = 0; j < i; j++) {
            if (a[i] > a[j] && order[i] <= order[j]) {
                order[i] = order[j] + 1;
            }
        }
    }

    max = *max_element(order.begin(), order.end());
    cout << max << endl;

    for (int i = n - 1; i >= 0; i--) {
        if (order[i] == max) {
            lis.push_back(a[i]);
            max--;
        }
    }

    while (!lis.empty()) {
        cout << lis.back() << " ";
        lis.pop_back();
    }

    return 0;
}

 
LIS를 출력하는 부분이 조금 다른데 그냥 O(n²)을 C++로는 좀 나중에 작성해서 더 깔끔해 보이는 쪽으로 고쳤다.
뭐로 하든지 출력은 잘 된다.