https://school.programmers.co.kr/learn/courses/30/lessons/12946
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
<문제>

<풀이>
이런 문제는 문제를 읽었을 때 어떻게 풀어야 할지 감이 잘 잡히지 않는다. 이러한 상황에서는 우선 문제를 시각화 해보자.

좌측은 n = 1일때, 우측은 n = 2일때의 이동을 시각화 한 것이다. 빨간색 숫자는 원판을 뜻하고 파란색 선은 이동루트를 뜻한다. n = 1 일 때는 당연한 이동 경로지만 n = 2일 때는 중간에 있는 기둥을 사용해야한다. 하지만 아직까진 규칙이 뚜렷하게 드러나지 않는다.
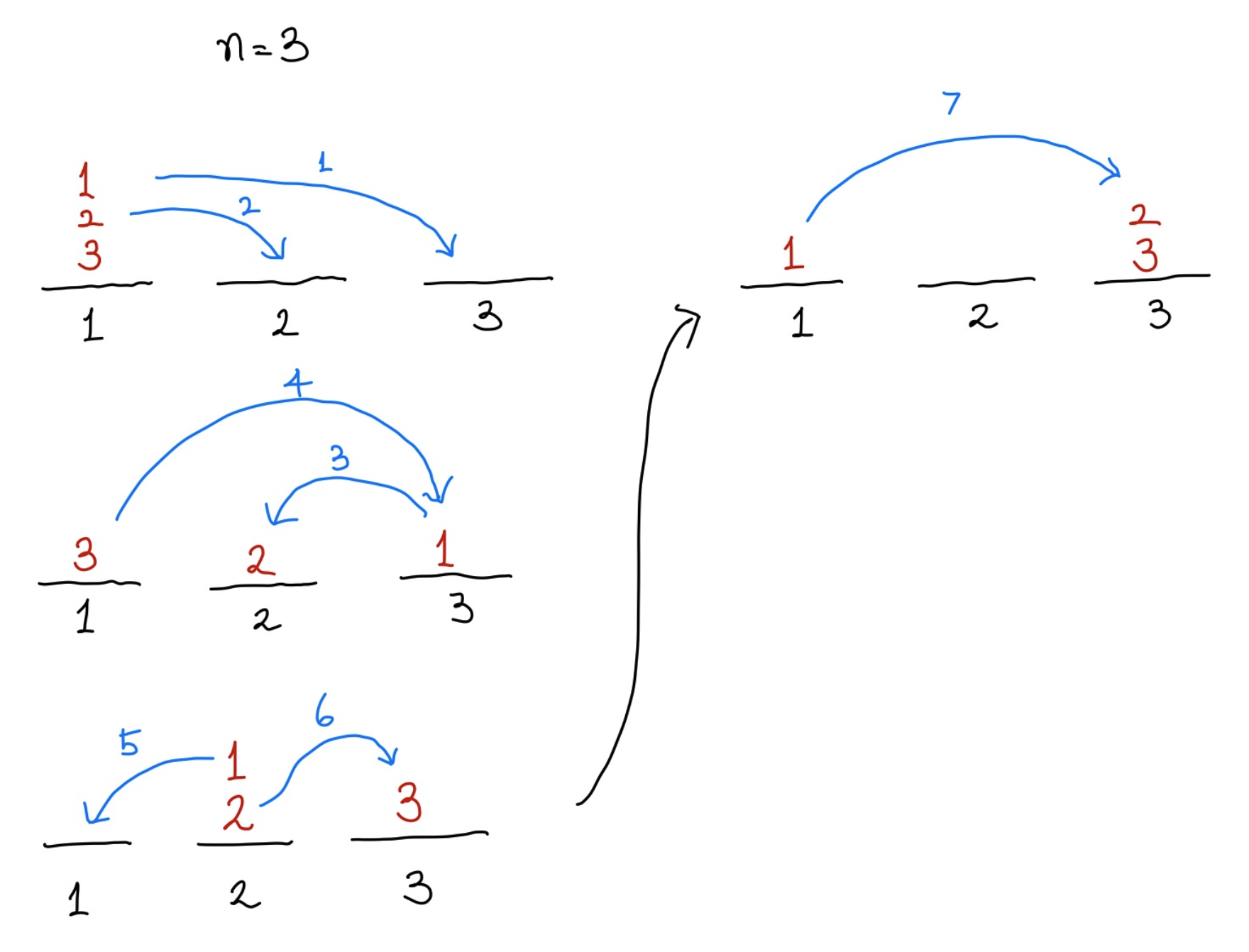
n = 3 일때의 이동경로를 시각적으로 나타냈다. 사실 직접 손으로 그리지 않고 다른 사람이 그린 그림으로 봤을 땐 아직도 규칙이 아리송 할 수 있지만 손으로 직접 그렸을 땐 규칙을 바로 알아 챌 수 있다.
그림에 표현하진 않았지만, 3번째 이동을 했을 때를 생각해보자, 그럼 2번째 기둥에 1, 2원반이 꽂혀 있고 1번째 기둥에 3번 원반이 꽂혀 있다. 그리고 1번 기둥에 꽂혀 있는 3번 원반을 3번 기둥으로 옮기면 아래 그림에 나타난 형상이 된다(4번째 이동을 했을 때)
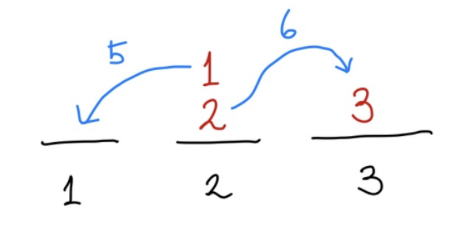
마지막으로 2번 기둥에 꽂혀있는 1, 2번 원반을 3번 기둥으로 옮기면 된다. 어떻게? n = 2일때랑 똑같다. 앞선 과정도 생각해보면 1, 2번 원반을 2번 기둥으로 옮기는 것 또한 n = 2일때랑 똑같다! 따라서 다음과 같은 규칙을 바로 알 수 있다.
1. n개의 원반이 있을 때 n 원반을 제외한 모든 원반(n - 1 원반까지)을 2번 기둥에 꽂는다.
2. n 원반을 3번 기둥으로 옮긴다
3. 2번 기둥에 꽂혀있는 1...n-1 원반을 3번 기둥에 꽂는다.
이 정도까지 왔으면 자연스럽게 재귀함수를 구성 할 수 있다. 우리는 n = 1이 어떻게 움직이는지 알고있기 때문에...
<코드>
import Foundation
func solution(_ n:Int) -> [[Int]] {
func hanoi(n: Int, start: Int, mid: Int, dest: Int) {
if n == 1 {
answer.append([start, dest])
return
}
hanoi(n: n - 1, start: start, mid: dest, dest: mid)
// 1...n-1 원반을 2번 기둥으로 옮기기
answer.append([start, dest])
// n 원판을 3번 기둥으로 옮기기
hanoi(n: n - 1, start: mid, mid: start, dest: dest)
// 1...n-1 원반을 2번 기둥에서 3번 기둥으로 옮기기
}
var answer: [[Int]] = []
hanoi(n: n, start: 1, mid: 2, dest: 3)
return answer
}
<ETC>

사실 본인도 n = 4까지 대충 그리고서야 규칙을 이해했다.
'Problem Solving > Swift' 카테고리의 다른 글
| [백준]BOJ 14502 - 연구소 - Swift/BFS & DFS (0) | 2023.07.05 |
|---|---|
| [백준]BOJ 1049 - 기타줄 - Swift/Greedy (0) | 2023.06.16 |
| [백준]BOJ 11000 - 강의실 배정 - Swift/Greedy (1) | 2023.06.16 |
| [백준]BOJ 16398 - 행성 연결 - Swift/MST (0) | 2023.02.25 |
| [백준]BOJ 4195 - 친구 네트워크 - Swift/Union-Find Set (0) | 2023.02.23 |




댓글